本系列笔记文章意在对《神经网络与深度学习》一书中学到的知识点进行浓缩和总结,并加入自己的理解。
《神经网络与深度学习》资源
英文版:http://neuralnetworksanddeeplearning.com/
中文版:https://pan.baidu.com/s/1mi8YVri 密码:e7do
一个人工神经元的结构

如上图所示,一个普通的人工神经元
- 有若干个输入($x_1, x_2,… x_n$),
- 只有一个输出值
从输入到输出的计算可以从下图看出

每个输入 $a_n$ 都对应着一个权重 $w_n$ 。每个神经元也都拥有自己的偏置值 $b$ 和一个非线性函数 $f$ (通常叫做激活函数 Activation Function)
具体的计算如下
将权重向量 $W = (w_1, w_2…w_n)$ 输入向量 $A = (a_1, a_2…a_n)^T$ 点乘得到的值加上偏置 $b$ 得到一个值 $z$。为了方便运算,我们也可以在输入向量 $A$ 后面添加一个1,这样就可以把偏置 $b$ 当做一个权重来看待。
$ z = w_1a_1 + w_2a_2 + … + w_na_n + b*1$
对 $z$ 套用激活函数 $f$ 得到 $output = f(z)$
S 型神经元
常用的S型神经元(也叫做逻辑神经元)就是使用sigmoid函数(也叫做逻辑函数,用符号 $σ$ 表示 )作为激活函数的神经元。
sigmoid函数表达式如下
$$ f(z) = \frac{1}{1 + e^{-z}} $$
sigmoid函数有一个非常好的性质就是
$$f’(z) = f(z)(1 - f(z))$$
图像如下

神经网络的架构及常用符号
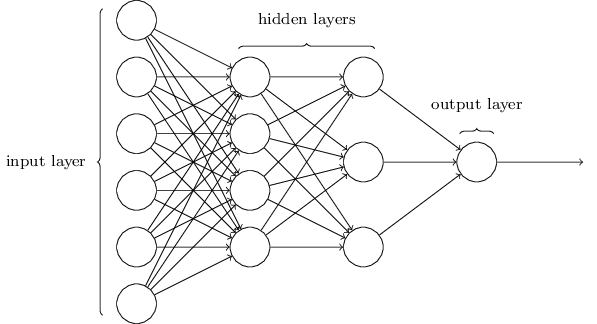
如上图所示,一个普通的前馈、全连接神经网络的架构可以分为三层:输入层,隐藏层和输出层。
前馈(feedforward)意味着神经网络中没有回路,信息总是向前传播。
全连接意味着同一层的神经元之间无连接,而层与层之间的神经元之间彼此都有连接。
特别要提的是
- 输入层的输入即输出,没有权重、偏置和激活函数
- 隐藏层层数大于等于两层的神经网络称为深度神经网络
- 一般来讲,多分类问题中,有几个输出类别,输出层就有几个神经元
- 按照是否允许网络中存在反馈回路可以将网络分为前馈神经网络和递归神经网络两类。相对简单,应用也最为广泛的是前馈神经网络。
神经网络的本质
神经网络的本质是一个庞大的多层嵌套复合函数
比如正如上面提到的,对于一个神经元,我们有
$$output = f(z)$$
$$z = w_1a_1 + w_2a_2 + … + w_na_n + b*1$$
而这个神经元的output可能也是下一层每个神经元的输入,以此类推,那么神经网络最终的输出值 $output$ 可以看做是关于所有输入 $a_1, a_2 .. a_n$的一个函数。
神经网络的前向传播即我们将已经向量化的数据 $(a_1, a_2 .. a_n)^T$ 输入到输入层,得到函数值 $output$ 的过程。
神经网络训练的本质
神经网络训练的本质就是找到合适的权重 $w$ 和偏置 $b$,使对于给定的输入 $x$,网络的输出 $a$ 可以拟合所有我们希望得到的输出 $y(x)$。
为了量化我们如何实现这个目标,我们定义一个代价函数(又称损失或目标函数):
$$C(w, b) ≡ \frac{1}{2n}∑||y(x) - a||^2$$
这里 $w$ 表示所有的网络中权重的集合,$b$ 是所有的偏置,$n$ 是训练输入数据的个数,$a$ 是表示当输入为 $x$ 时输出的向量,求和则是在总的训练输入 $x$ 上进行的。符号 $∥v∥$ 是指向量 v 的模。 我们把 $C$ 称为二次代价函数;有时也称被称为均方误差或者 MSE。观察二次代价函数的形式我 们可以看到 $C(w, b)$ 是非负的,因为求和公式中的每一项都是非负的。此外,当对于所有的训练输入 $x$,$y(x)$ 接近于输出 $a$ 时, $C(w, b) ≈ 0$。因此如果我们的学习算法能找到合适的权重和偏置,使得 $C(w, b) ≈ 0$,网络就能很好地工作。相反, 当 $C(w, b)$ 很大时就不怎么好了,那意味着对于大量地输入,$y(x)$ 与输出 $a$ 相差很大。因此我们训练神经网络的目的,是要找到一系列能让代价函数 $C$ 尽可能小的权重和偏置。
梯度下降算法
从某个意义上来讲,训练神经网络就是找到代价函数 $C(w, b)$ 的最小值点。因为常见的神经网络通常有包含数量庞大的权重的偏置的代价函数,极其复杂,所以用微积分来解析最小值是不可能的。通常我们会用称为梯度下降的算法来达成目的,
设想我们此时的代价函数是一个二元函数 $C(v_1, v_2)$
那么根据微积分有
$$∆C ≈ \frac{∂C}{∂v_1}∆v_1 + \frac{∂C}{∂v_2}∆v_2$$
让我们来定义 $v$ 的变化量向量 $∆v ≡ (∆v_1, ∆v_2)^T$,同时 $C$ 的偏导数向量 $(\frac{∂C}{∂v_1}, \frac{∂C}{∂v_2})^T$,即为 $C$ 的梯度向量,记为 $∇C$:
$$∇C ≡ (\frac{∂C}{∂v_1}, \frac{∂C}{∂v_2})^T$$
梯度是一个向量,指向函数值增长最快的方向。详细解释可参考这里
此时,$∆C$ 的表达式可以被重写为:
$$∆C ≈ ∇C · ∆v$$
假设我们选取:
$$∆v = -η∇C$$
这里的 $η$ 是个很小的正数(称为学习速率,Learning Rate)。那么就有$∆C ≈ −η∇C·∇C = −η∥∇C∥^2$。 由于 $∥∇C∥^2 ≥ 0$,这保证了 $∆C ≤ 0$,即,如果我们按照 $∆v = -η∇C$ 去改变 $v$,那么 $C$ 会 一直减小,不会增加。(当然,要在 $∆C ≈ ∇C · ∆v$ 的近似约束下)。
最终我们可以得到为了使 $C$ 减小的 $v$ 的改变规则:
$$v→v′= v−η∇C$$
用权重和偏置来替换变量 $v_j$, 我们就得到了神经网络中运用梯度下降算法对权重和偏置的更新规则。
$$w_k→w_k′ =w_k−η\frac{∂C}{∂w_k} $$
$$b_l →b′_l =b_l −η\frac{∂C}{∂b_l} $$
重复应用这一规则,就有望能找到代价函数的最小值,即让神经网络学习。
更多梯度下降的解释和例子可以参考这里
随机梯度下降 (Stochastic Gradient Descent)
普通梯度下降的问题
让我们回顾前面提到的二次代价函数形式
$$C(w, b) ≡ \frac{1}{2n}∑||y(x) - a||^2$$
注意到这个代价函数有着这样的形式 $C = \frac{1}{n} ∑ Cx$,即它是遍及每个训练样本代价 $Cx ≡ \frac{||y(x) - a||^2}{2}$的平均值。在实践中,为了计算梯度 $∇C$,我们需要为每个训练输入 $x$ 单独地计算梯度值 $∇Cx$,然后求平均值,$∇C = \frac{1}{n} ∑_x∇Cx$。不幸的是,当训练输入的数量过大时会花费很⻓时间,这样会使学习变得相当缓慢。
换句话说,就是普通梯度下降中,每一次对权重和偏置进行更新,我们都需要把全部的训练输入放到神经网络中,得到对于每一条输入 $x$ 的输出 $a_x$,再结合代价函数求 $∇C_x$,最终得到训练数据整体的 $∇C = \frac{1}{n} ∑_x∇Cx$ 来更新权重和偏置。这样训练集一大就很慢。
随机梯度下降的思想
随机梯度下降(SGD)的思想就类似于统计中的随机抽样来反映整体。
SGD的具体操作为,首先将全部训练数据打散(随机排序),然后将其分成一个个固定大小的片(batch),然后遍历每个batch,对这个batch内的每一条数据求其 $∇C_x$,然后平均得到整体的 $∇C$ 来更新权重和偏置。
反应到具体的公式就是
$$∇C ≈ \frac{1}{m}\Sigma_{j=1}^m∇C_{X_j}$$
$$w_k→w_k′= w_k−\frac{η}{m}\Sigma_j\frac{∂C_{X_j}}{∂w_k}$$
$$b_l→b_l′= b_l−\frac{η}{m}\Sigma_j\frac{∂C_{X_j}}{∂b_l}$$
这里 $m$ 是batch的大小,$j$ 代表 batch中的某一条数据。
Batch, Iteration, Epoch的定义
- Batch:将训练数据随即打散然后按固定大小分割成的数据片叫做一个batch,其大小就是batch_size
- Iteration: 利用一个batch中的数据对权重和偏置的一次更新叫做一个iteration
- Epoch:当全部的batch都被便利了一遍,此时就叫一个epoch。
零散的知识点
- 随机梯度下降和误差反向传递不适合直接用来训练深度神经网络
- 复杂的算法 ≤ 简单的算法 + 好的训练数据